Lab 8: Binary Search Trees

Learning outcomes

By the end of this lab, students will be able to:

• Write recursive methods to solve tasks for binary search trees (non-mutating and mutating)
• Analyse the runtime efficiency of binary search tree tree methods using simple profiling

In this lab, you will gain even more practice with recursion by implementing some methods that act on binary search trees.

Task 0: Setup and review

Download bst.py and profile_bst.py into your labs/lab8 folder.

Review

We now have gone from general trees to binary trees, in which every item in the tree has at most two children. We also introduced the binary search tree (BST) property, which is when an item is >= all values in its left subtree, and <= all values in its right subtree. A binary search tree is a binary tree for which every item has the BST property.

Our implementation of the BST class removes the _subtrees attribute of general trees, and replaces it with explicit _left and _right attributes, whose values are the left and right subtrees (which are themselves BSTs). Again, this is a recursive data structure, and so our code often has the following form:

    def my_bst_method(self) -> ...:
        if self.is_empty():
            ...
        else:
            ... self._root ...
            ... self._left.my_bst_method() ...
            ... self._right.my_bst_method() ...

But if our method also takes an item, we often compare this item against the root, and then use the BST property to determine what to do next:

    def my_bst_method(self, item: Any) -> ...:
        if self.is_empty():
            ...
        elif item == self._root:
            ...
        elif item < self._root:
            ...
        else:  # item > self._root
            ...

Of course, the hard work is figuring out how to fill in and modify these templates to get the desired behaviour, as you’ll work through on this lab.

Preparation for recursion!

Before starting the exercises, make sure you do the following. Trust us, it will make reasoning about your code much easier later on.

Take a blank sheet of paper, and draw (with circles and arrows) the following:

• An empty BST (just write the word “Empty” or something)
• A BST with just one item (any value in the item)
• A BST with a root item, a non-empty left subtree, and an empty right subtree
• A BST with a root item, an empty left subtree, and a non-empty right subtree
• A BST with a root item, and left and right subtrees both with height >= 2

Keep these in mind as scenarios that your methods must handle.

Task 1: Non-mutating methods

Open bst.py. To warm up, read the docstring and implement the height method, which returns the height of a BST. Remember that our definition of height counts the number of items, not the number of edges (parent-to-child connections), on the longest path from the root to a leaf of the tree. Note: think carefully about whether or not you can use the BST property here to reduce the number of recursive calls.

Then, read the docstring for items_in_range, which is similar to the items and smaller methods from this week’s prep. The docstring requires you to ensure that the list is returned in the correct order; do not use a built-in list.sort method or function to accomplish this. Instead, you should exploit the fact that a BST is already “sorted”.

Remember our recursive design technique: write out what the recursive calls on each subtree would return, and think about how to combine these to get the final result.

Task 2: BST insertion

Now let’s look at one fundamental mutating method for Binary Search Trees: inserting a new value into the tree. Notice that this method does not return anything. When we make a recursive call, we won’t be relying on it to report back some value to us. Instead, we will rely on it to mutate something for us.

The simplest approach for inserting into a BST is to preserve the existing structure of the tree by putting the new item at the “bottom” of the tree, by making it a leaf.

It turns out to be quite straightforward to implement this type of insertion recursively:

1. If the BST is empty, simply make the new item the root of the tree.
2. Otherwise, the item should be inserted into either the left subtree or the right subtree. (Certainly not both!) How can you use the BST property to figure out where the item should go?

If you need a hint, think back to how __contains__ is implemented!

Task 3: Timing experiments

For this task, you will run some experiments to measure the efficiency of the BST methods insert and delete, and look at how these depend on the order in which items are inserted. Open profile_bst.py, and finish the provided code to run some timing experiments on BST insertion and deletion that investigate how the insertion order affects running time.

Are any of the experiments particularly slower than the others? Why do you think this is? Try looking at the heights of the trees that are constructed—you should find that they are quite lopsided.

Task 4: Rotations

Depending on our implementations, repeated insertions and deletions can leave a BST looking very imbalanced, which hurts the efficiency of these operations (we’ll discuss this more in lecture). One strategy to resolve this imbalance is to change the structure of the tree itself; we’ll explore one simple version of this for the last part of today’s lab.

A rotation is a mutation of a BST that changes the structure of the tree around the root. In a rotation, the root value is demoted to a subtree, and a child of the root, called the pivot, is promoted to become the new root.

We will look at right rotations and left rotations. In a right rotation, the left child of the root is the pivot, and after the rotation becomes the new root, as in the before and after images below:

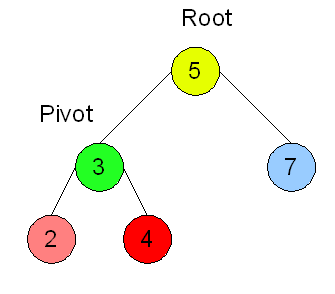
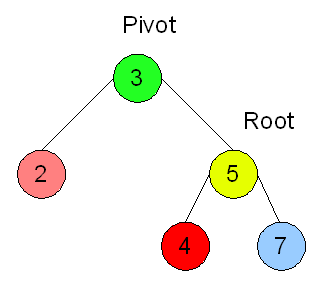
In a left rotation, the right child of the root is the pivot, and after the rotation becomes the new root, as in these before and after images:

Wikipedia has a helpful animation that helps illustrate rotations.

Your task here is to implement a left and a right rotation. Before you start writing any code, draw a few examples of a tree, and practice rotating it to the left, and to the right. Write down the steps involved in a left rotation, then write the steps involved in a right rotation.

Only after you’re confident that you can do these rotations manually should you begin to implement the rotate_left and rotate_right methods.

Tips:

1. These methods are not recursive. Instead, they’re an exercise in working carefully with BinarySearchTree attributes.
2. You may create new BinarySearchTrees when implementing these methods.
3. Use parallel assignment (x, y = 1, 2) to help streamline the mutations in your code.

With careful use of your rotation methods, it is possible to write insertion and deletion methods that ensure that a BST’s height remains small compared to its size. You’ll learn all about this in CSC263!

Additional tasks

Iteration

Even though trees are naturally recursive structures, it is possible to use a loop to process them. This takes significantly more work, but is an interesting challenge if you’re looking for something to do on a Friday night. ;)

Print out the value of every item in a binary search tree, in any order you want, without using recursion.

You might find it helpful to use a data structure that we have already covered in this class.